The four-parameter Weibull functions

'W1.4' and 'W2.4' provide the four-parameter Weibull functions, self starter function and names of the parameters.

W1.4(fixed = c(NA, NA, NA, NA), names = c("b", "c", "d", "e"), ...)

  W2.4(fixed = c(NA, NA, NA, NA), names = c("b", "c", "d", "e"), ...)

Arguments

fixed	numeric vector. Specifies which parameters are fixed and at what value they are fixed. NAs for parameter that are not fixed.
names	a vector of character strings giving the names of the parameters. The default is reasonable.
...	additional arguments to be passed from the convenience functions.

Details

The equations for the mean functions are given at weibull1.

Value

See weibull1.

References

Seber, G. A. F. and Wild, C. J (1989) Nonlinear Regression, New York: Wiley \& Sons (pp. 330--331).

Ritz, C (2009) Towards a unified approach to dose-response modeling in ecotoxicology To appear in Environ Toxicol Chem.

Note

This function is for use with the model fitting function drm.

Examples


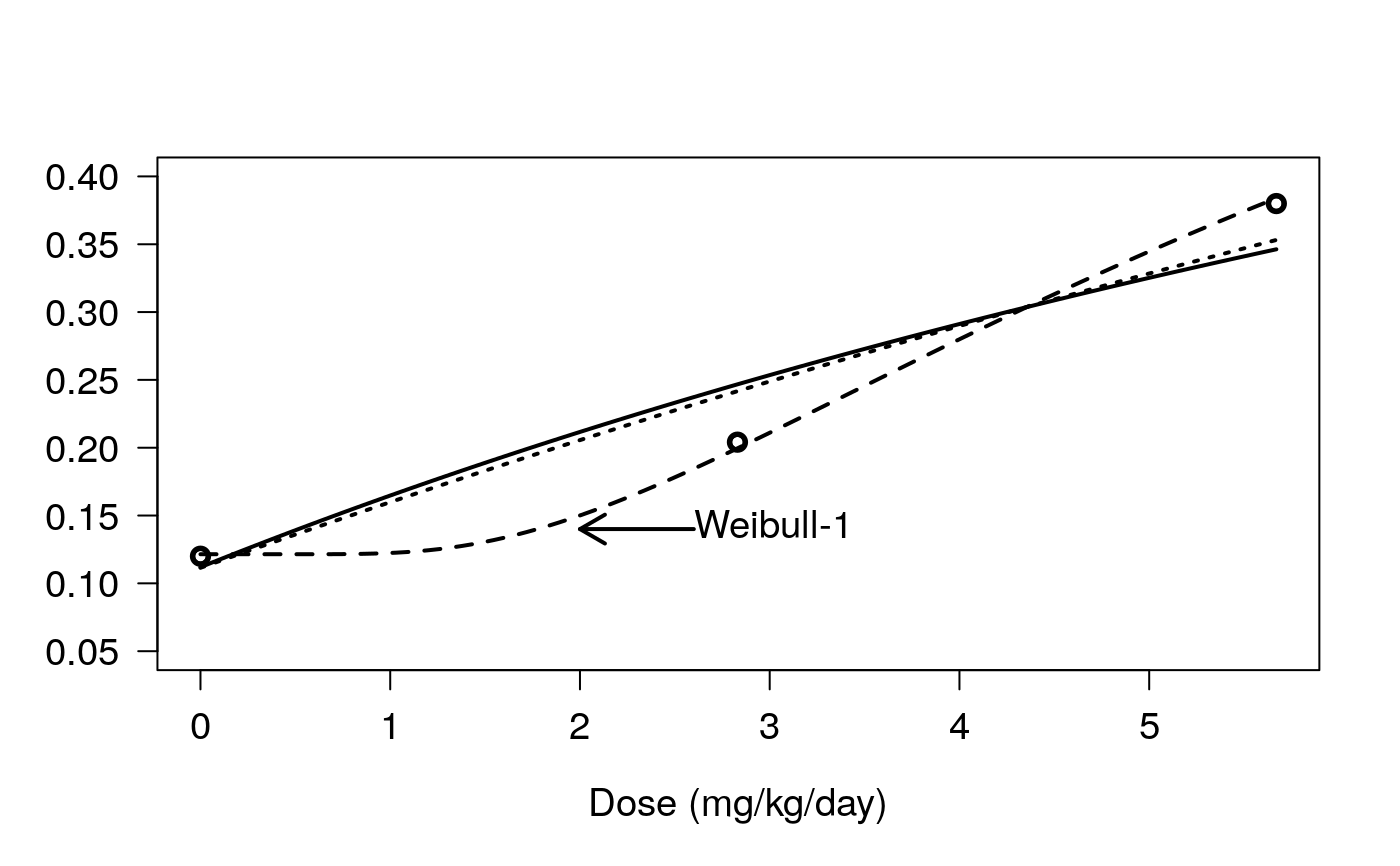
## Fitting a four-parameter Weibull (type 1) model
terbuthylazin.m1 <- drm(rgr~dose, data = terbuthylazin, fct = W1.4())
summary(terbuthylazin.m1)
#> 
#> Model fitted: Weibull (type 1) (4 parms)
#> 
#> Parameter estimates:
#> 
#>                 Estimate Std. Error t-value   p-value    
#> b:(Intercept) 9.7401e-01 1.4451e-01  6.7401 3.753e-07 ***
#> c:(Intercept) 2.4632e-02 1.4782e-02  1.6663    0.1076    
#> d:(Intercept) 3.0889e-01 9.5904e-03 32.2080 < 2.2e-16 ***
#> e:(Intercept) 2.5485e+02 4.0604e+01  6.2766 1.211e-06 ***
#> ---
#> Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
#> 
#> Residual standard error:
#> 
#>  0.02694557 (26 degrees of freedom)

## Fitting a first-order multistage model
## to data from BMDS by EPA
## (Figure 3 in Ritz (2009))
bmds.ex1 <- data.frame(ad.dose=c(0,50,100), dose=c(0, 2.83, 5.67),
num=c(6,10,19), total=c(50,49,50))

bmds.ex1.m1<-drm(num/total~dose, weights=total, data=bmds.ex1,
fct=W2.4(fixed=c(1,NA,1,NA)), type="binomial")

modelFit(bmds.ex1.m1)  # same as in BMDS
#> Goodness-of-fit test
#> 
#>             Df Chisq value p value
#>                                   
#> DRC model    1     0.57224  0.4494

summary(bmds.ex1.m1)  # same background estimate as in BMDS
#> 
#> Model fitted: Weibull (type 2) (2 parms)
#> 
#> Parameter estimates:
#> 
#>                Estimate Std. Error t-value  p-value   
#> c:(Intercept)  0.111475   0.041719  2.6721 0.007539 **
#> e:(Intercept) 17.860515   5.919727  3.0171 0.002552 **
#> ---
#> Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

logLik(bmds.ex1.m1)
#> 'log Lik.' -6.179627 (df=2)

## BMD estimate identical to BMDS result
## BMDL estimate differs from BMDS result (different method)
ED(bmds.ex1.m1, 10, ci="delta")
#> 
#> Estimated effective doses
#> 
#>        Estimate Std. Error
#> e:1:10  1.88179    0.62371

## Better fit

bmds.ex1.m2<-drm(num/total~dose, weights=total, data=bmds.ex1,
fct=W1.4(fixed=c(-1,NA,1,NA)), type="binomial")
modelFit(bmds.ex1.m2)
#> Goodness-of-fit test
#> 
#>             Df Chisq value p value
#>                                   
#> DRC model    1    0.010589   0.918
summary(bmds.ex1.m2)
#> 
#> Model fitted: Weibull (type 1) (2 parms)
#> 
#> Parameter estimates:
#> 
#>               Estimate Std. Error t-value   p-value    
#> c:(Intercept) 0.121468   0.044268  2.7439  0.006071 ** 
#> e:(Intercept) 6.850273   1.540986  4.4454 8.774e-06 ***
#> ---
#> Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

ED(bmds.ex1.m2, 50, ci = "delta")
#> 
#> Estimated effective doses
#> 
#>        Estimate Std. Error
#> e:1:50   9.8829     2.2232

## Creating Figure 3 in Ritz (2009)
bmds.ex1.m3 <- drm(num/total~dose, weights=total, data=bmds.ex1,
fct=LL.4(fixed=c(-1,NA,1,NA)), type="binomial")

plot(bmds.ex1.m1, ylim = c(0.05, 0.4), log = "", lty = 3, lwd = 2,
xlab = "Dose (mg/kg/day)", ylab = "",
cex=1.2, cex.axis=1.2, cex.lab=1.2)

mtext("Tumor incidence", 2, line=4, cex=1.2)  # tailored y axis label

plot(bmds.ex1.m2, ylim = c(0.05, 0.4), log = "", add = TRUE, lty = 2, lwd = 2)

plot(bmds.ex1.m3, ylim = c(0.05, 0.4), log = "", add = TRUE, lty = 1, lwd = 2)

arrows(2.6 , 0.14, 2, 0.14, 0.15, lwd=2)
text(2.5, 0.14, "Weibull-1", pos=4, cex=1.2)