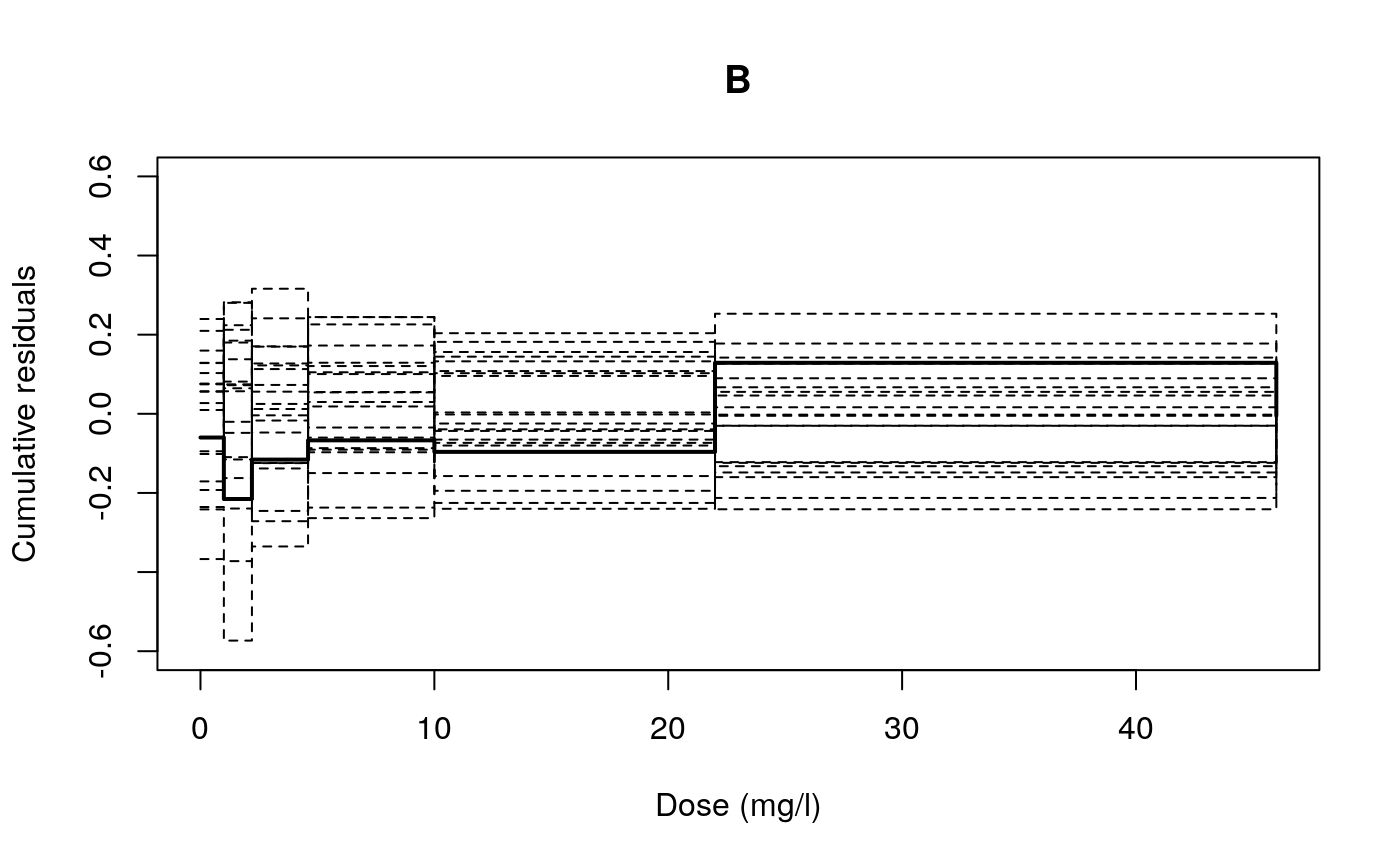
Lack-of-fit test for the mean structure based on cumulated residuals
lin.test.RdThe function provides a lack-of-fit test for the mean structure based on cumulated residuals from the model fit.
lin.test(object, noksSim = 20, seed = 20070325, plotit = TRUE, log = "", bp = 0.01, xlab, ylab, ylim, ...)
Arguments
| object | object of class 'drc'. |
|---|---|
| noksSim | numeric specifying the number of simulations used to obtain the p-value. |
| seed | numeric specifying the seed value for the random number generator. |
| plotit | logical indicating whether or not the observed cumulated residual process should be plotted. Default is to plot the process. |
| log | character string which should contains '"x"' if the x axis is to be logarithmic, '"y"' if the y axis is to be logarithmic and '"xy"' or '"yx"' if both axes are to be logarithmic. The default is "x". The empty string "" yields the original axes. |
| bp | numeric value specifying the break point below which the dose is zero (the amount of stretching on the dose axis above zero in order to create the visual illusion of a logarithmic scale including 0). |
| xlab | string character specifying an optional label for the x axis. |
| ylab | character string specifying an optional label for the y axis. |
| ylim | numeric vector of length two, containing the lower and upper limit for the y axis. |
| … | additional arguments to be passed further to the basic |
Details
The function provides a graphical model checking of the mean structure in a dose-response model. The graphical display is supplemented by a p-value based on a supremum-type test.
The test is applicable even in cases where data are non-normal or exhibit variance heterogeneity.
Value
A p-value for test of the null hypothesis that the mean structure is appropriate. Ritz and Martinussen (2009) provide the details.
References
Ritz, C and Martinussen, T. (2009) Lack-of-fit tests for assessing mean structures for continuous dose-response data, Submitted manuscript
See also
Other available lack-of-fit tests are the Neill test (neill.test) and
ANOVA-based test (modelFit).
Examples
## Fitting a log-logistic model to the dataset 'etmotc' etmotc.m1<-drm(rgr1~dose1, data=etmotc[1:15,], fct=LL.4()) ## Test based on umulated residuals lin.test(etmotc.m1, 1000)#> [1] 0.074#lin.test(etmotc.m1, 10000, plotit = FALSE) # more precise ## Fitting an exponential model to the dataset 'O.mykiss' O.mykiss.m1<-drm(weight~conc, data=O.mykiss, fct=EXD.2(), na.action=na.omit) ## ANOVA-based test modelFit(O.mykiss.m1)#> Lack-of-fit test #> #> ModelDf RSS Df F value p value #> ANOVA 54 17.620 #> DRC model 59 18.492 5 0.5351 0.7488## Test based on umulated residuals lin.test(O.mykiss.m1, log = "", cl = 0.2, xlab = "Dose (mg/l)", main = "B", ylim = c(-0.6, 0.6))#> Warning: "cl" is not a graphical parameter#> Warning: "cl" is not a graphical parameter#> Warning: "cl" is not a graphical parameter#> Warning: "cl" is not a graphical parameter#> Warning: "cl" is not a graphical parameter#> Warning: "cl" is not a graphical parameter#> [1] 0.65#lin.test(O.mykiss.m1, noksSim = 10000, plotit = FALSE) # more precise