The Cedergreen-Ritz-Streibig model

'cedergreen' provides a very general way of specifying then Cedergreen-Ritz-Streibig modified log-logistic model for describing hormesis, under various constraints on the parameters.

CRS.6 is the extension of link{cedergreen} with freely varying alpha parameter.

For u-shaped hormesis data 'ucedergreen' provides a very general way of specifying the Cedergreen-Ritz-Streibig modified log-logistic model, under various constraints on the parameters.

cedergreen(fixed = c(NA, NA, NA, NA, NA),
  names = c("b", "c", "d", "e", "f"),
  method = c("1", "2", "3", "4"), ssfct = NULL,
  alpha, fctName, fctText)

  CRS.6(fixed = c(NA, NA, NA, NA, NA, NA),
  names = c("b","c","d","e","f","g"),
  method = c("1", "2", "3", "4"), ssfct = NULL)

  ucedergreen(fixed = c(NA, NA, NA, NA, NA),
  names = c("b", "c", "d", "e", "f"),
  method = c("1", "2", "3", "4"), ssfct = NULL,
  alpha)

Arguments

fixed	numeric vector. Specifies which parameters are fixed and at what value they are fixed. NAs for parameter that are not fixed.
names	a vector of character strings giving the names of the parameters (should not contain ":"). The order of the parameters is: b, c, d, e, f (see under 'Details').
method	character string indicating the self starter function to use.
ssfct	a self starter function to be used.
alpha	numeric value between 0 and 1, reflecting the steepness of the hormesis peak. This argument needs to be specified.
fctName	optional character string used internally by convenience functions.
fctText	optional character string used internally by convenience functions.

Details

The model is given by the expression

$$ f(x) = c + \frac{d-c+f exp(-1/(x^{\alpha}))}{1+exp(b(log(x)-log(e)))}$$

which is a five-parameter model (alpha is fixed or freely varying). Not all features (eg EC/ED calculation) are available for the model with freely varying alpha.

It is a modification of the four-parameter logistic curve to take hormesis into account.

The u-shaped model is given by the expression

$$ f(x) = cd - \frac{d-c+f \exp(-1/x^{\alpha})}{1+\exp(b(\log(x)-\log(e)))}$$

Value

The value returned is a list containing the non-linear function, the self starter function and the parameter names.

References

Cedergreen, N. and Ritz, C. and Streibig, J. C. (2005) Improved empirical models describing hormesis, Environmental Toxicology and Chemistry 24, 3166--3172.

Note

The functions are for use with the functions drm.

See also

For fixed alpha, several special cases are handled by the following convenience functions CRS.4a, CRS.4b, CRS.4c, CRS.5a, CRS.5b, CRS.5c, UCRS.4a, UCRS.4b, UCRS.4c, UCRS.5a, UCRS.5b, UCRS.5c where a, b and c correspond to the pre-specified alpha values 1, 0.5 and 0.25, respectively.

Examples

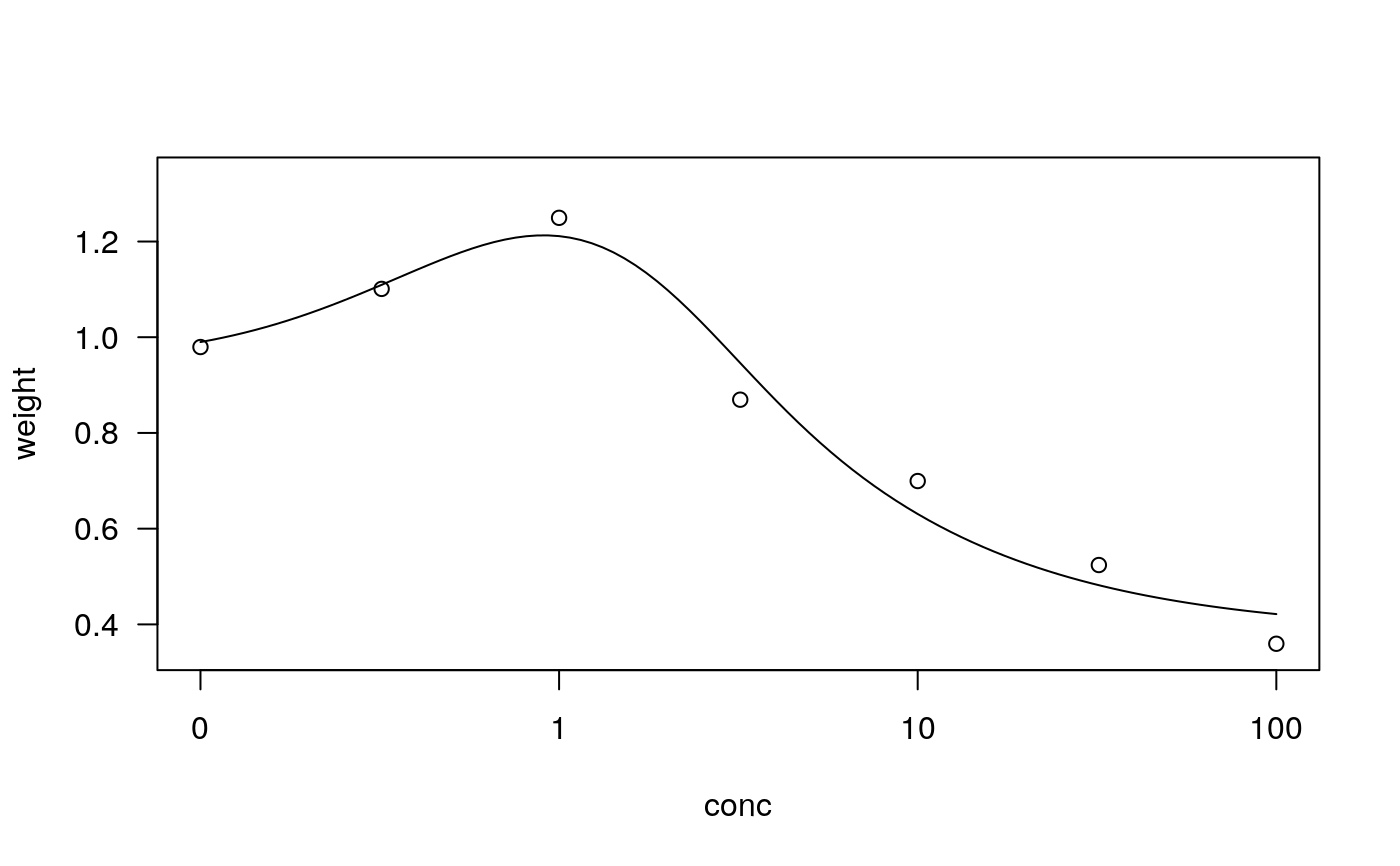
## Estimating CRS model with alpha unknown
lettuce.crsm1 <- drm(weight~conc, data = lettuce, fct = CRS.6())
summary(lettuce.crsm1)
#> 
#> Model fitted: Generalised Cedergreen-Ritz-Streibig (hormesis) (6 parms)
#> 
#> Parameter estimates:
#> 
#>               Estimate Std. Error t-value p-value  
#> b:(Intercept)  0.81093    0.34482  2.3518 0.04655 *
#> c:(Intercept)  0.38074    0.12504  3.0450 0.01594 *
#> d:(Intercept)  4.44821    7.36988  0.6036 0.56285  
#> e:(Intercept)  0.34664    1.09141  0.3176 0.75891  
#> f:(Intercept) -3.46826    7.37262 -0.4704 0.65061  
#> g:(Intercept) -1.15917    0.49533 -2.3402 0.04740 *
#> ---
#> Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
#> 
#> Residual standard error:
#> 
#>  0.1243802 (8 degrees of freedom)
plot(lettuce.crsm1)  # oops: not increasing until hormesis peak