Michaelis-Menten model

The functions can be used to fit (shifted) Michaelis-Menten models that are used for modeling enzyme kinetics, weed densities etc.

MM.2(fixed = c(NA, NA), names = c("d", "e"), ...)

  MM.3(fixed = c(NA, NA, NA), names = c("c", "d", "e"), ...)

Arguments

fixed	numeric vector. Specifies which parameters are fixed and at what value they are fixed. NAs for parameter that are not fixed.
names	a vector of character strings giving the names of the parameters (should not contain ":").
...	additional arguments from convenience functions to llogistic.

Details

The model is defined by the three-parameter model function

$$f(x, (c, d, e)) = c + \frac{d-c}{1+(e/x)}$$

It is an increasing as a function of the dose \(x\), attaining the lower limit \(c\) at dose 0 (\(x=0\)) and the upper limit \(d\) for infinitely large doses. The parameter \(e\) corresponds to the dose yielding a response halfway between \(c\) and \(d\).

The common two-parameter Michaelis-Menten model (MM.2) is obtained by setting \(c\) equal to 0.

Value

A list of class drcMean, containing the mean function, the self starter function, the parameter names and other components such as derivatives and a function for calculating ED values.

Note

At the moment the implementation cannot deal with infinite concentrations.

See also

Related models are the asymptotic regression models AR.2 and AR.3.

Examples

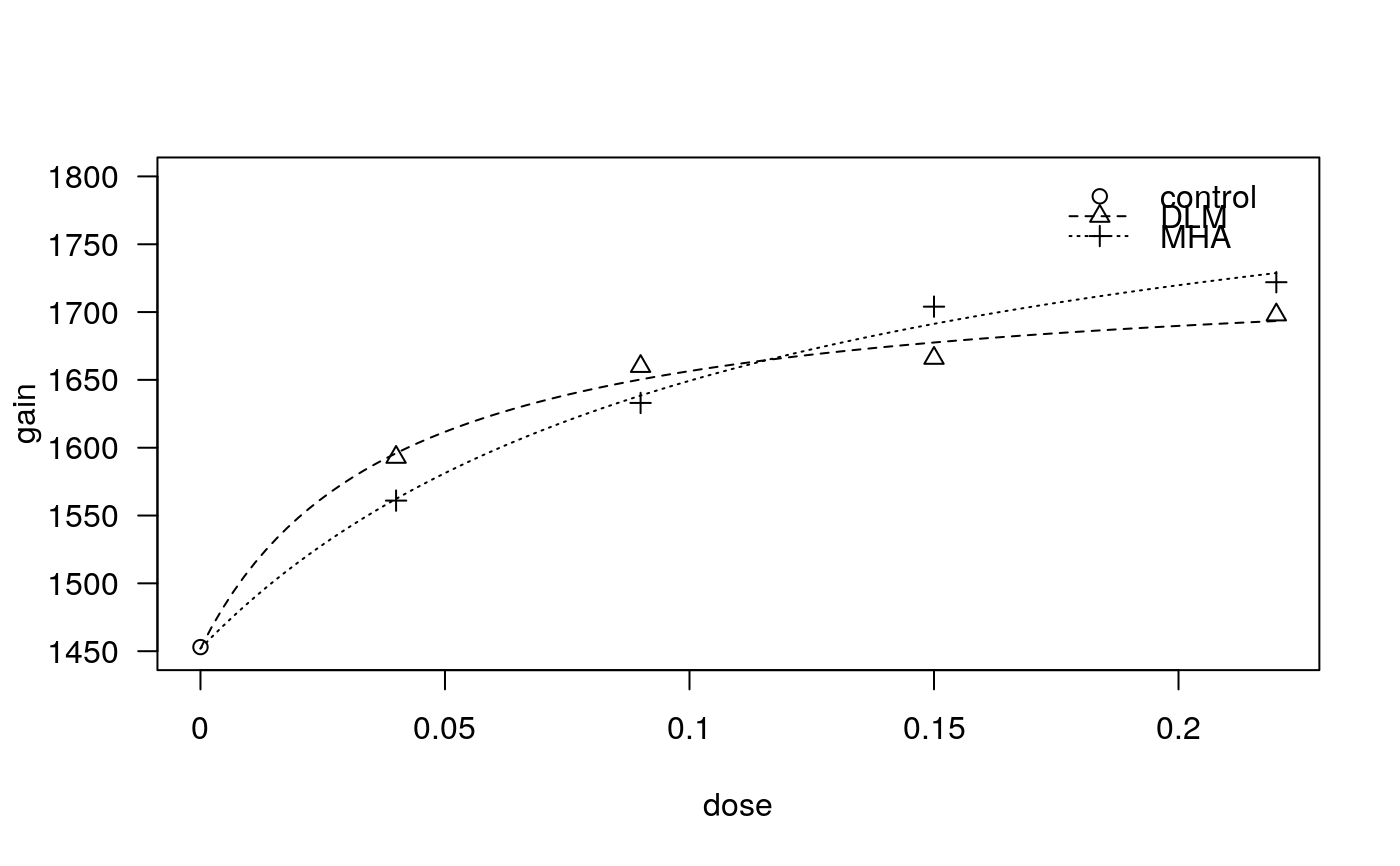
## Fitting Michaelis-Menten model
met.mm.m1 <- drm(gain~dose, product, data=methionine, fct=MM.3(),
pmodels = list(~1, ~factor(product), ~factor(product)))
#> Control measurements detected for level: control
plot(met.mm.m1, log = "", ylim=c(1450, 1800))
summary(met.mm.m1)
#> 
#> Model fitted: Shifted Michaelis-Menten (3 parms)
#> 
#> Parameter estimates:
#> 
#>                 Estimate Std. Error  t-value   p-value    
#> c:(Intercept) 1.4520e+03 1.0886e+01 133.3830 1.895e-08 ***
#> d:DLM         1.7361e+03 1.8922e+01  91.7543 8.459e-08 ***
#> d:MHA         1.8685e+03 4.3930e+01  42.5337 1.826e-06 ***
#> e:DLM         3.8946e-02 1.0184e-02   3.8241   0.01871 *  
#> e:MHA         1.1104e-01 2.8484e-02   3.8984   0.01757 *  
#> ---
#> Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
#> 
#> Residual standard error:
#> 
#>  11.14285 (4 degrees of freedom)
ED(met.mm.m1, c(10, 50))
#> 
#> Estimated effective doses
#> 
#>           Estimate Std. Error
#> e:DLM:10 0.0043274  0.0011316
#> e:DLM:50 0.0389462  0.0101843
#> e:MHA:10 0.0123379  0.0031649
#> e:MHA:50 0.1110410  0.0284837

## Calculating bioefficacy: approach 1
coef(met.mm.m1)[4] / coef(met.mm.m1)[5] * 100
#>    e:DLM 
#> 35.07368 

## Calculating bioefficacy: approach 2
EDcomp(met.mm.m1, c(50,50))
#> 
#> Estimated ratios of effect doses
#> 
#>                 Estimate Std. Error    t-value    p-value
#> DLM/MHA:50/50  0.3507368  0.1181319 -5.4960893  0.0053418

## Simplified models
met.mm.m2a <- drm(gain~dose, product, data=methionine, fct=MM.3(),
pmodels = list(~1, ~factor(product), ~1))
#> Control measurements detected for level: control
anova(met.mm.m2a, met.mm.m1)  # model reduction not possible
#> 
#> 1st model
#>  fct:     MM.3()
#>  pmodels: ~1, ~factor(product), ~1
#> 2nd model
#>  fct:     MM.3()
#>  pmodels: ~1, ~factor(product), ~factor(product)
#> 
#> ANOVA table
#> 
#>           ModelDf     RSS Df F value p value
#> 1st model       5 1794.73                   
#> 2nd model       4  496.65  1 10.4546  0.0319

met.mm.m2b <- drm(gain~dose, product, data=methionine, fct=MM.3(),
pmodels = list(~1, ~1, ~factor(product)))
#> Control measurements detected for level: control
anova(met.mm.m2b, met.mm.m1)  # model reduction not possible
#> 
#> 1st model
#>  fct:     MM.3()
#>  pmodels: ~1, ~1, ~factor(product)
#> 2nd model
#>  fct:     MM.3()
#>  pmodels: ~1, ~factor(product), ~factor(product)
#> 
#> ANOVA table
#> 
#>           ModelDf     RSS Df F value p value
#> 1st model       5 1885.43                   
#> 2nd model       4  496.65  1 11.1851  0.0287